Travelling Salesman Problem (TSP): Given a set of cities and distance between every pair of cities, the problem is to find the shortest possible route that visits every city exactly once and returns to the starting point.

Cities in this example are represented as vertices and roads between them are the edges. Hence, we have an undirected graph and edges are weighted (distance between them).

This is an NP-Hadr problem, which means that it can only be solved in exponential time. Therefore, we cannot find an optimal solution, but we can approximate the solution using approximation algorithms.

What we are looking for in this problem is the Hamiltonian cycle, which means that we may visit each vertex exectly once and we must return to the starting vertex.

There are two different algorithms to solve this problem:

1. MST-DFS Method (2-approximation algorithm)
2. Christofides’ ALgorithm (3/2-approximation algorithm)

MST-DFS method

1. Start with a complete weighted graph

                                                        

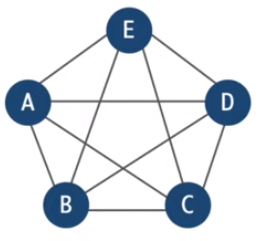
1. Find Minimum Spaning Tree

   Use Kruskal’s or Prim’s algorithm to find the MST. Once the MST is built, perform DFS traversal on it.

                                                           

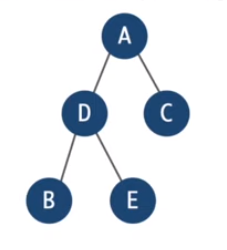
2. Do a DFS Traversal

   A -> D -> B -> D -> E -> D -> A -> C -> A

   We can see that we are revisiting vertices 2 times. We will avoid that in the following step.

3. Delete Duplicate Vertices

   A -> D -> B -> E > C -> A

   Now we have the Kamiltonian cycle.

This method gives us some solution that is greater or equal than the optimal solution and less than or equal to 2 * MST. Since in the step 3 we visited each edge twice, which gives us 2 minimum spanning trees, which is the worst case scenario. On the other side, the best case scenario is when we traverse through one MST.

Optimal Solution <= MST tour found <= 2 * MST

Since the worst case scenario is 2 * Optimal Solution, we call this a 2-approximation algorithm.

Christofides’ ALgorithm

Give the following graph:

                                                        

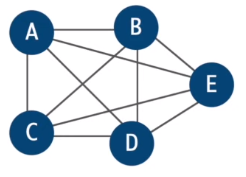
Steps in this agorithm:

1. Find a minimum spanning tree T

                                                           

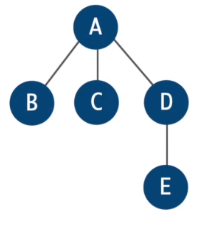
2. Let O be the set of vertices with odd degree in T. Find minimum-cost perfect matching M.

                                                           

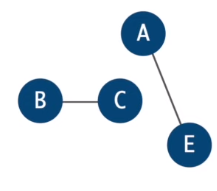
In this step we are keeping only the vertices with the odd degree (odd number of vertices attached to it). Then, we connect the vertices with minimal cost pairing.

1. Add the set of edges of M to T. Find an Eulerian tour.

This means that we are looking for a tour that covers every edge. A -> B -> C -> A -> E -> D -> A

                                                        

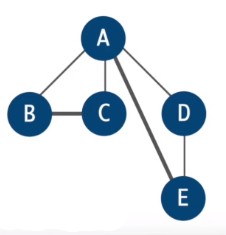
1. Shortcut the Eulerian tour to amke a Hamiltonian Cycle.

In this step we are removing duplicates since duplicates in the path mean that we are visiting the same vertex multiple times.

A -> B -> C -> E -> D -> A

                                                        

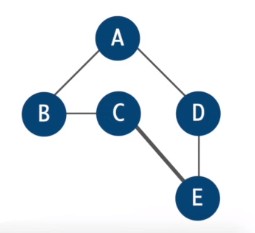
We finaly got the solution to the problem.