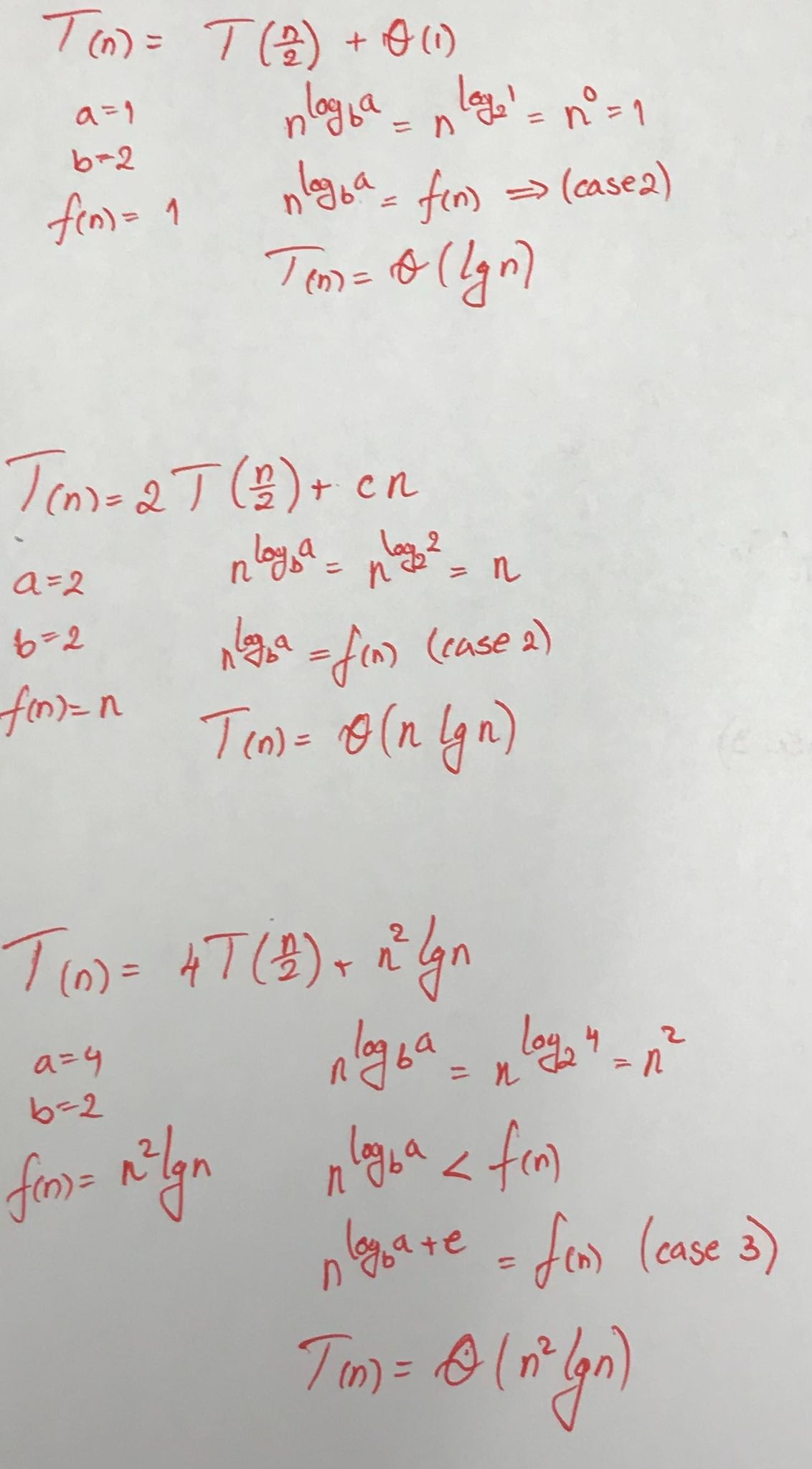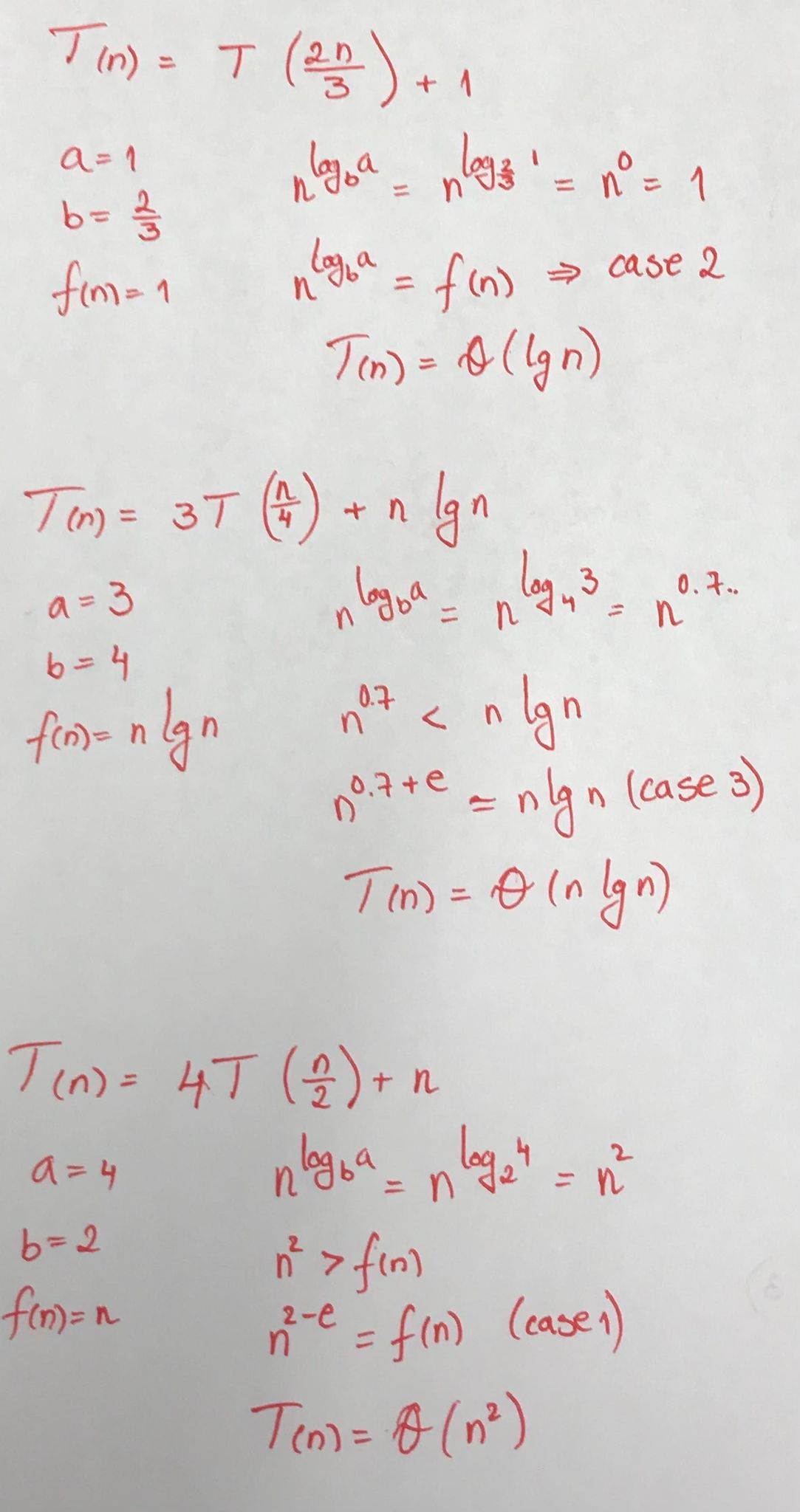The Master Method - Reccurences
In this method, the recurrences are solved in the following form:
T(n) = aT(n-b) + f(n)
where a>= 1, b>= 1 are the constraints and f(n) is an asymptotically positive function.
The reccurence describes the running time of an algorithm that divides a problem of size n into a subroblems , each of size n/b.
The a subproblems are solved recursively, each in time T(n/b).
f(n) represents a function that defines the cost of dividing the problem and combining results of the subproblems
Rules:
- If f(n) = O(n^log_b(a-e)) for some constant e > 0, then T(n) = Θ(n^log_b(a))
- If f(n) = O(n^log_b(a)), then T(n) = Θ(n^log_b(a)* lg(n))
- If f(n) = O(n^log_b(a+e)) for some constant e > 0, then T(n) = f(n)